Botany online 1996-2004. No further update, only historical document of botanical science!
The science of control and information is called cybernetics. Control and exchange of information, also called communication, takes place in all systems. The term system covers both the system elements and their interactions. These generate the system properties. The theory covering the behaviour of systems is called system theory. Systems that live in a continuous exchange with their environment are called open systems . All living systems are open and in a steady state. This means that they are never in an stationary equilibrium.
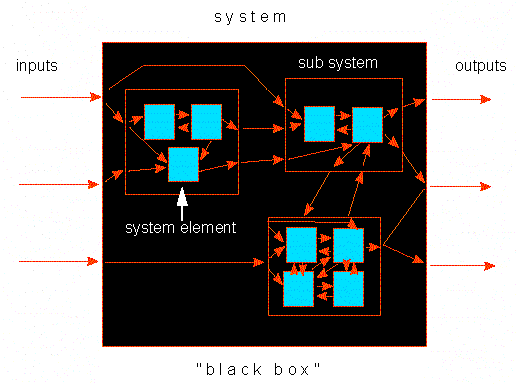
The system theory allows the description of system elements as 'black boxes' that are characterized by only their output and input. Such a system element is also called a transitional element. Every system has a certain capacity, too big input signals may consequently lead to damage or disruption of the system.
Two types of systems exist: deterministic and probabilistic systems. Deterministic systems have elements that co-operate in a predictable way, probabilistic systems can never be fully understood and thus only be described in a probabilistic way.
The English term control covers two German terms: 'Regelung'
(regulation) and 'Steuerung' (instruction), that are clearly defined
and set off against each other. 'Steuerung' behaves towards
'Regelung' like a straight line to a circle. N. WIENER coined the
term cybernetics in 1948. He used
it to describe the science of control and information independent of
whether this takes place in living organisms or machines. Control
phenomenons are widespread in biology. There is- to be exact- no
living system (cell, organism, ecosystem) that is not controlled. All
quantities involved are in direct or indirect relation and do thus
form a net of mutual dependence.
The term system covers both
the elements of function and their interactions. The functional
relations of the system elements cause the specific properties and
capacities of a system: the system
properties. The single system elements can be grouped
together to depict a system in a block diagram
since block diagrams are instructive aids for the understanding of
the nature of the system's elements and their combinations. They form
the basis for a further system-analytic analysis of the data. They
serve to stocktake facts and represent the structure of the effects.
There are a whole range of structures and processes in biology that
can be depicted in this way.
A system consists of a number of system
elements. It is important to distinguish system elements
that range at the same level from such of higher or lower levels of
hierarchy. Systems of lower levels are sub-systems of a higher
system. Living systems, for example, can be arranged according to the
following hierarchy:
The system 'cell' that ranges at the lowest level (cells are the basic elements of all living things) is itself made from non-living molecules. Based on their complexity and size, it is distinguished between small molecules and macromolecules. Macromolecules can be united in supramolecular complexes (often with the aid of small molecules): ribosomes, chromosomes, membranes and others. One level higher are the organelles: mitochondria, chloroplasts and others.
All these components and their interactions cause the system properties of a cell. To explain the system 'living cell', a complete list of all components (nature and number) and a list with all interactions, or, in other words with all metabolic activities of a cell is needed. These requirements exceed our possibilities and we do therefore have to be content with partial answers. But we will see that the system theory offers possibilities to use also incomplete sets of data as a basis for reliable statements.
Living systems require the continuous uptake of energy and
nutriments from their environment, to excrete and to react in
specific ways. Cells have therefore -just like all other biological
systems- to be regarded as open
systems that are characterized by inputs and outputs and
an in-between element of transition. They are never in a stationary
equilibrium but always in a steady
state. As long as we do not know what happens in the
transitional element (in our case
the cell) it can, according to the system theory, be regarded as a
black box. The relation between
input and output characterizes a flow of information through the
system. A physical or chemical energy may influence the system
through the input and thus cause certain changes that may again have
an influence on other systems or system elements via the
output. From a cybernetic point of view, neither the inner structure
of the transitional element (in the case of the cell: the
requirements mentioned above) nor the form of the energy is of
importance. The time course of input and output signal and the
connection of both signals alone is decisive.
Transitional elements or systems do in the simplest case operate
linearly; the input and the output signal would thus be proportional.
But their function is usually much more complex so that the output
signal is noticeably changed. Such changes can be captured
mathematically and can be described by formulas that are normally
differential and integral equations of first or higher orders. This
means that the output signal may have any state.
Among the system properties of a plant cell is growth. We may regard it as an output. Inputs would be chemical and physical quantities like nutriments, light, temperature and others. Since a plant cell itself constitutes only a partial system of the higher level system tissue, its reaction is also influenced by the behaviour of the neighbouring cells. As we have already seen, growth itself can therefore not be captured as a constant quantity and no mathematical formula exists that would be equally valid for all cells of a plant tissue.
A very important factor for the description of transitional systems is time. An input signal may lead to a delayed output signal. Transitional systems may therefore have a kind of memory if they are complex enough, in which the input signals are settled by addition or multiplication.
The system may, for example, react with a threshold that has to be passed by the input signals before an output signal is generated. But every system has only a limited capacity. This means that the input signal may not be too strong without causing reversible or irreversible damage of the system's function. A too high temperature, for example, destroys a cell and all its system properties with it. To understand the system 'cell', it is hence not enough to know the qualitative course of the effects' connections but a number of fixed and variable quantities have also to be taken into account. Among them are the time the chemical reactions need, the time needed for signal transmission, diffusion and permeability constants and certain enhancing factors that describe the connection between cause and effect quantitatively, for example the influence of a catalyst (an enzyme) onto the reaction time. The measuring of such quantities within a working system is very difficult since the measurings cannot be performed without disruption of the course of reactions. And it is exactly here that the advantage of the mathematical approach becomes clearly recognizable. It enables intern factors to be considered. Numerous parameters can be varied in model calculations in order to simulate the reaction of the system, to outline its capacities and, if need be, to predict future developments, for example inappropriate reactions. Namely, the functional course of a system is not that much dependent on the chosen mechanisms but much more on the achieved result. Based on this premise, it is useful to construct a model to understand the nature of a complex system. The more properties (including the limit and the inappropriate reactions) two systems (original and model) share the more do also their functional elements resemble each other.
Although such considerations are basically unlimited by mathematics and although many mathematical considerations can be realized in technical areas, it is - as hopefully the preceding exposition shows - extremely difficult to capture biological transitional systems by mathematical equations. A mathematician may develop a system that displays certain properties of a living system but it will still be far away from considering all its properties.
It is distinguished between deterministic and probabilistic (stochastic) systems. The deterministic ones have elements that co-operate in a predictable way, like technical machines do. Probabilistic systems cannot be fully understood; their results are merely probable but can never be predicted exactly. Living systems are always probabilistic, since we do not know all of their elements and since they are always made from partial systems of different functional levels.
Attempts of the system theory serve especially to explain dynamic processes and to understand the flow of material, energy and information. They are, as will be shown later, very useful for the understanding of ecological networks. Plants are considered to be primary producers in all ecosystems since only they are able to transform solar into chemical energy. Consumers, specially animals, need the chemical energy produced by the plants for their own growth and survival. Energy flows of these kinds are thus decisive quantities for the description of ecosystems.
This approach neglects completely the way in which the plant transforms the energy, which plant species are especially efficient and which part a certain plant species has in the energy flow. These and many other problems are put into the black box 'plant' since only the amount of energy or the quality of the product is of interest to the consumer. This example shows the approach of the system theory. Never are all components and interactions regarded at the same time, instead it is concentrated on a certain question that can be solved with the existing means.