
Botany online 1996-2004. No further update, only historical document of botanical science!

For many biologists, the microscope belongs to the gadgets they use most. The reason is obvious: cells are the basic units of life and their size is, with only few exceptions, below the upper limit of the resolution of the human eye. Numerous statements on the refraction of light by lenses or waterfilled spheres and the resulting magnification proof, that the effects of magnification were already known in antiquity. In the 13th century, the British natural scientist ROGER BACON used segments of glass spheres as magnifying glasses and recommended them to partially sighted persons as spectacles. The grinding of lenses was perfected in the following centuries.
The physician P. BORCH records, that HANS and ZACHARIAS JENSEN (father and son) from the Dutch town Middelburg invented the compound microscope at the beginning of the 17th century by placing one lens behind the other. They are regarded as the inventors of the telescope, too. Other sources name C. J. DREBBEL (1572 - 1634) from Alkmaar as the inventor of the microscope. Even if this should not be the case, he has helped a lot to make the microscope known. The term microscope was introduced by members of the Italian Accademia de Lincei (Academy of The Lynx), whose most prominent member was G. GALILEI.
Independent of the beginning development of the two-lensed - also called the compound microscope - stronger and stronger lenses became fashionable, too. Again, it was a Dutchman, A. van LEEUWENHOEK, who succeeded in the construction of lenses with 270 fold magnification and a focal length of about one millimetre, with which he worked. His resulting observations constitute the pinnacle of "single-lensed microscopes".
In 1667, the "Micrographia" of the British natural scientist ROBERT HOOKE was published. HOOKE examined vegetable tissues with the help of a compound microscope and thus detected their basic elements, the cells. The further development of microscopes and especially the use of microscopes in the 18th century went on rather hesitantly. This was on one hand caused by the opinion of many natural scientists of reputation, that a lot had still to be discovered even without the use of microscopes. On the other hand, the interfering chromatic aberrations were a continuing source of misinterpretations. This led to the prejudice, that anything you wanted to see could be seen within a microscope.
As soon as 1695, D. GREGORY considered the combination of several lenses with differing dispersions in order to minimise this handicap. The mathematician L. EULER brought forth a theoretical explanation of achromates (systems of lenses with corrected colors) in 1771 and he suggested the calculation of such achromatic objectives. They were finally built by F. G. BEELDSNYDER (1735 - 1808), who placed a biconcave lens out of flint glass between two biconvex lenses out of another type of glass, that had a different index of refraction.
G. D. AMICI (1786 - 1863) developed achromatic systems of lenses further and invented also immersion objectives. The actual break-through on the way to the construction of modern microscopes was due to the formulation of a theory of image formation within the microscope by E. ABBÉ (1840 - 1905). He proved, that an absolute upper limit of microscopic image formation exists and that it was dependent of the aperture of the objective and the wave length of the light. His theory permitted the development of reproducible high-performance microscopes and their production in series.
The use of newly developed types of glasses by O. SCHOTT (1851 - 1935) led in 1886 to the development of apochromatic objectives (objectives, that remove a rest of colors, the so-called secondary spectrum) by E. ABBÉ and C. ZEISS.
The progress of microscope building enabled a quick series of numerous discoveries in the subjects of histology, cytology and bacteriology. The progress was helped by the development and use of suitable methods of fixation, embedding and cutting, specific dyes and conservatives.
The closer an object is to the eye, the more details can be distinguished until the limit is reached, below which the eye cannot depict the object clearly any more. This limit is 250 mm for the average grown-up. The measure for the ability to tell two points apart is called the power of resolution. It describes whether two adjoining points can still be perceived as separate. To examine objects below this limit of resolution, a magnifying glass is needed. Its magnification can be calculated in the following way:
250 mm is the image distance of the human eye and f is the focal length of the lens. If the magnifying power of the lens is known and the focal length has to be calculated, than the formula has to be used as shown beneath:

The picture to the left shows the way the fan of rays of an object
that is collected by a single lens is imaged.
If you want to magnify an object even more, two lenses in tandem have to be used (objective and eyepiece or ocular). The resulting construct is a simple microscope. The objective magnifies the object or specimen (O) and a turned up real image (O´) is formed in front of the focal plane of the second lens. The eyepiece than forms an enlarged virtual image (O''), that can be seen as a turned up image at a distance of 250 mm. The magnification of a microscope is thus a product of
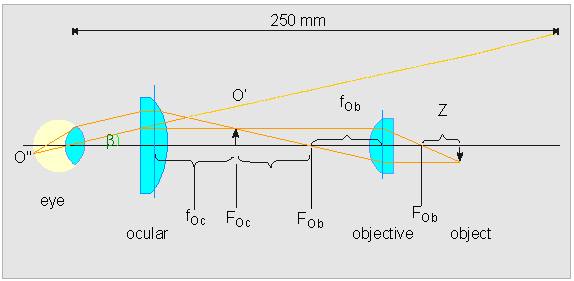
Light path in the microscope: F = Focal plane, O = Object (Specimen), Ob = Objective, Oc = ocular (eyepiece)
Nonetheless the power of resolution is given exclusively by the objective. To describe an objective not only the magnifying power has to be taken in account, but, too, the numerical aperture. The numerical aperture is defined as the sine of half the angle of the cone of light from each point of the object, that can be accepted by the objective (alpha) multiplied by the index of refraction of the medium in which the object is immersed (n):
The medium is usually air with a refraction index of n = 1. alpha can never be bigger than 90° and thus the numerical aperture can never outgrow 1. Its largest actual size is 0.95, since the distance between objective and the surface of the cover glass cannot reach zero. The aperture of 0.95 corresponds to an angle alpha of roughly 72°. An increase of the numerical aperture can be achieved by the choice of a medium between objective and object with an index of refraction bigger than that of air. Special oil for immersion with an index of n = 1.515 has proved to be useful. Larger indexes of refraction do not make sense, because the index of refraction of the objective itself (n = 1.525) becomes limiting. Immersion oil can be used only with specially constructed immersion objectives. If alpha has the maximum of 67.5°, the aperture is accordingly 1.515 x 0.92 = 1.40. The degree of resolution (d) is set by the wavelength of light (lambda) and the numerical aperture (Aobj):
If lambda is 550 nm (green light) the formula runs the following way:
0.2 Ám is the highest theoretical resolution that can be reached with a light microscope. A rough approximation shows that the power of resolution of a light microscope lies at about half the length of a lightwave if a good immersion objective is used. If the limit of resolution of a microscope is known, then the maximal useful magnification can be calculated. A magnification is called useful when two only just clear points are magnified so strongly that they are seen as separate unities by the human eye. At 250mm is the resolution of the human eye about 0.15 - 0.2 mm. The rule of thumb for a useful magnification is thus:
An objective with an aperture of 1.4 has accordingly a maximal useful magnification of 1400fold.
We assume that the dual nature of light as both wave and particle is known and we will in the following deal with some fundamental principles of wave optics in order to be able to interpret microscopic image formation. Our main interest, nevertheless, is the understanding of modern techniques of light microscopy like phase-contrast microscopes, polarising microscopes and interference microscopes. First some terms and definitions:
Amplitude, frequency, wave length, interference, diffraction and phase are the most important parameters to describe a wave. The wavelength of visible light is between 400 and 800 nm. Interference is the mutual influence of two waves on each other, whereby the resulting crests may be either enhanced or flattened (enhancement of amplitude, reduction of amplitude). The extreme case is given by two waves that extinguish each other.
Diffraction is the partial deflection of a ray of light at the corners of opaque objects. For understanding it is useful to cast a look at phenomenons of diffraction at simple gap- or hole-shaped masks. If a screen is placed behind such a mask and light is sent through, the pattern of diffraction can be seen. It consists of a regular pattern of points or lines that fades away towards the margins. The shape of the pattern is dependent on the kind of mask and the object used (for example a microscopic preparation). But the pattern is always grouped around a central axis (unmagnified picture of the gap or hole of the mask). If a mask with two openings is used, the light is diffracted at the rim of both openings. The diffraction images of the two rays overlie each other and regular enhancements and reductions can be seen in the resulting pattern. To get a magnified image, the first additional maxima of the diffraction image have to be included (E. ABBÉ). The results in the pictures above have already shown that the distances of the points in a diffraction image are reversed proportional to the corresponding distances in the object. To gain a real image from a diffraction image a collecting lens (the objective of the microscope is one) is needed. This lens has to have a big enough aperture to collect the intensity maxima (-I, +I). The real image is formed by both refracted and non-diffracted light.
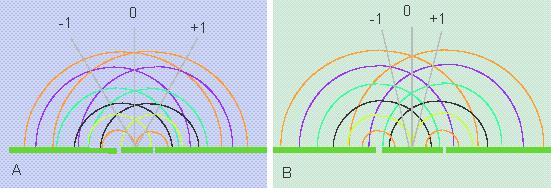
Diffraction phenomenon at apertures. The closer two openings (or diaphragms) that diffract light are, the larger is the angle of the diffraction's first intensity maxima and the larger has the aperture of the collecting lens to be.
Magnifications as those that have been described can, too, be achieved with radiation of other natures. The most important additional device for biologists besides the light microscope is the electron microscope, where the diffraction of a ray of electrons is used. Another radiation to be mentioned is the short-waved Röntgen-radiation (X ray-radiation), that has proven to be of value for the elucidation of molecular structures (M. v. LAUE, L. BRAGG). Since no collecting lenses for Röntgen-radiation exist, the information contained in the diffraction pattern has to be calculated mathematically in order to get to know the structure of the molecule.