How Do You Analyze Ecosystems ?

Ecosystems are usually stochastic systems, on one hand, because they depend on a variety of different parameters, some of which, but never all can be captured. On the other hand are they stochastic, because they are always open systems. Their most important members, the organisms, depend on a steady supply of energy. Two conceptionally different methods to gain information about ecosystems and biocenoses exist.

1. stocktaking:

	capture of (all) species of a habitat,
	determination of the percentages of the single species,
	determining of changes in the species composition as a function of time (a. during the cycle of the year, b. over a longer period of time),
	determination and capture of all those chemical and physical parameters, that the organisms depend upon.

Stocktaking has a long tradition. Mapping of vegetation and plant geography are just two methods to be mentioned here. You can find more about stocktaking in the topic plant societies.

2. systems analysis:

The attempt by systems analysis is younger than stocktaking. The advent of cybernetics during the 1940^th resulted in aids that help defining systems and system properties mathematically in order to develop models suitable for predictions.

Both attempts - stocktaking and systems analysis - complement each other. Only if the results gained by both methods are taken into consideration, it can be tried to understand an ecosystems and to recognize its balance, its behavior, and its sensitivity towards disruptions as well as to comprehend future developments.

The fundamental principles of the system theory are discussed in the chapter about cybernetics. Here, we will only give some additions and an illustrating example.

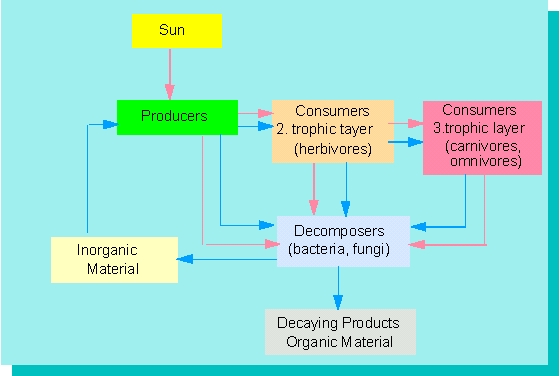
Simplified model of an energy and material flow occurring within an ecosystem. The material flow (blue lines) is a circuit, the flow of energy (red lines) is linear.

1. The system elements, in this case the producers, the consumers of the first order, the consumers of the second order, and the decomposers are arranged one after the other. The arrangement is hierarchical. The single levels of hierarchy are called trophic levels.

2. 2. The system elements are interconnected by a flow of energy and material. The flow of energy is a linear process, the flow of material is a circuit.

Only plants and a few microorganisms are able to convert light energy into chemical energy. They are therefore called producers or primary producers, P. All other organisms are consumers of the first, second or third order or dor decomposers, also called saprophytes. The life-style of producers is called autotropic, the life-style of consumers is heterotropic. A mathematical description of an ecosystem requires four basic elements:

1. System variables (v_i) are a group of variables (v₁, v₂ ... v_n) that describe the state of the system at a given time. Among them are, for example, the biomass (in gram, kilogram, or tons dry weight per square or volume unit). v₁ describes thus the producers (P), v₂ the consumers of the first order, v₃ the consumers of the second order (carnivores, for example).

2. Transfer functions (F_i) are equations that describe the material turnover of a system. They cover, for example, that part of the biomass that is lost by respiration or that part that is used to feed the organisms at the next higher trophic level. The changes of a system variable as a function of time can be described by this differential equation:

dv_i / dt = f (v₁, v₂.......... vn, F₁, F₂... F_n)

3. Inputs are amounts of energy or material that are available for a system, like the amount of useable sun energy, the limiting amount of minerals in the soil or the temperature as a factor determining reactions. If only the transfer functions from one trophic level to the next higher one are of interest, then the corresponding F_i becomes the input. The amount of herbivores, for example, is decisive for the amount of carnivores.

4. Proportional factors (c_i) and constant factors are unchangeable. Among them is the amount of food an animal needs per period of time.

The mathematical model of a system can now be given by a set of equations that describe the flow of energy and material between the single levels. Matrix calculation is used in order to sum up sets of data and equations. A matrix is a two-dimensional list of data, where each value can be described by its co-ordinates i and j. Matrices can be multiplied with each other. The result is a new matrix. Such a mathematical description shows, for example, which system component has a direct influence on another one. In our generalized ecosystem, this would result in an image that shows that each system component has an effect on itself, but that carnivores, for example, have no direct influence on plants.

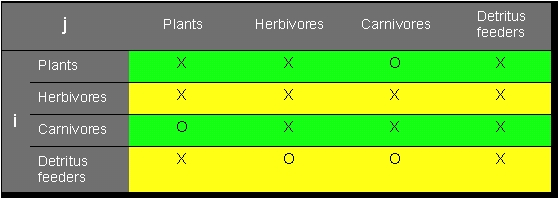
Ecological research produces always large amounts of data. It does therefore make sense to make them suitable for the computer, i.e. to group them right from the beginning into matrices that can easily be processed by the computer. No exact sets of data can be collected for many of the required parameters. The inputs fluctuate usually very much, due to unpredictable weather conditions, for example. The number of interactions occurring in a natural ecosystem is usually bigger than those given in its model. Animals cannot be clearly grouped into herbivores or carnivores as many of them are omnivores. But if such complications are recognized, it is relatively easy to integrate them into an existing system. Often, nevertheless, the necessary information is lacking. On the other hand, relations exist that have hardly any quantitative input. It does make sense to not consider them in the model in order to decrease the amount of work.

Until now, very few ecosystems have been described that show the properties of the system exemplarily. In Germany, there is a lake, the Plußsee in the vicinity of Plön/ Holstein, Germany, that can be cited as an example of an almost completely explored ecosystem (the work was done by the Max-Planck-Institute of Limnology at Plön, Germany). The "Solling-project" is an example of a terrestrial ecosystem, a wood, that is analyzed by researchers at the University of Göttingen, Germany.

The majority of ecologists have a solid knowledge of plant and animal species, but know only little about soil bacteria and fungi (decomposers). Hardly any data about their species composition, their population density, and their rate of multiplication under natural conditions do therefore exist. Kinetics of multiplication that were taken under lab conditions are only of partial use as those growth conditions are usually better and the rate of multiplication is thus higher than under natural conditions.

Attempts of system analysis can optimized so much that little and incomplete information becomes sufficient to make relatively apt predictions. Ecology depends on optimization processes comparable to those of projections done during elections, since all lists of data however extensive they may look represent always just a relatively small spot check of the actual not yet captured data. The accuracy of a mathematical model increases with increased complexity, while an ecosystem becomes more stable the more complex its is. Statistics shows that a systematic mistake (s) is inverse proportional to the root of the number of single measurements (1/ roots of n). The larger the amount of data, the smaller is consequently the error rate.